Security of Bitcoin and other PoW blockchains
It’s been almost 9 months since my previous blog, but in Bitcoin time it must have felt like decades. While the Earth was barely completing three third of its course around the Sun, thousands of Initial Coin Offerings (ICOs) have come and also vanished (or busted) with so much money that rival the previous dot-com bubble. Riding on Ethereum, an ICO typical issues digital tokens to be used as assets or utilities, and attracts investors with unspoken promises of many X increases in token values.
John Oliver described the current blockchain and cryptocurrency landscape quite eloquently:
everything we don’t understand about money combined with everything we don’t understand about computers.
In this post I’ll focus on explaining the current state of knowledge regarding security of these
cryptocurrencies. Security is often lauded as the key advantage of Bitcoin and Ethereum over the traditional
banking systems, i.e. cryptocurrencies are more secure. Well, if it were that cut and dry, I wouldn’t be
writing this. My hope is that given what we know about the current (in)security, you (readers) may understand
more about the computers parts and become more suspicious confused amazed at how this whole thing
(i.e. money) even work, let alone having billions of market capitalization.
I’ll start with some background on security of PoW blockchains. I’ll then discuss two important build-up work [1], [2] leading up to the formalization in [3], and end with the quantitative model in [4]. There are other important papers, but the selected are ones that I could make through, barely.
A little background
Blockchain is the buzz word of the day (a close second is AI). There are two main classes of blockchain systems: permissioned and permissionless. The former include Hyperledger, JP Morgan’s Quorum and Microsoft’s Coco. The latter — the original blockchain v1.0 — are made hugely popular by Bitcoin and Ethereum. One key difference between these two classes of systems is the consensus protocol. I have blogged more than once about consensus protocols in traditional distributed systems, i.e. how difficult and subtle they are. Traditional can be roughly understood as before Bitcoin. More specifically, traditional consensus protocols assume that every node knows about the identity of another node in the system. Permissioned blockchain makes adopt this assumption and therefore are able to use such protocols as PBFT without change.
Permissionless blockchains make no assumption about node’s identity. In such a purely decentralized setting, overcoming Sybil attack is challenging, and for which traditional consensus protocols cannot be applied. Proof of Work (PoW) emerges as the solution for achieving consensus. In PoW, nodes compete to solve computationally hard puzzles, and whoever finds a solution get to append a new block to the chain. One typical puzzle is to find \(n\) such that
\[\text{SHA256}(X||n) < D\]for a given value of \(X\) (hash of previous block) and \(D\) (pre-defined difficulty). In Bitcoin, \(D\) is set such that the average time of solving the puzzle, of the entire network as a whole, is about \(10\) minutes. \(D\) is adjusted dynamically based on the timestamps of a certain number of previous blocks. For example, if the previous $K$ blocks suggests fast block time (\(< 10\) minutes), \(D\) is decreased in order to bring the average block time back to \(10\) minutes. Maintaining an appropriate value for block time is in fact very important for security, as will be clear later.
A detailed comparisons of permissioned vs. permissionless blockchain merits a separate post. I’d shamelessly refer readers to my recent survey paper [5].
What is security?
Consensus protocols determine security of blockchain systems. In classic Byzantine settings, where malicious (or Byzantine) nodes behave arbitrarily, security is the same as safety when the number of Byzantine nodes is bounded. It broadly means that all honest nodes agree on the same value. In PBFT, for example, safety property dictates that if an honest node locally commits to a tuple \((seq,v)\), then all other honest nodes also do the same.
In PoW, the adversary model is also Byzantine. However, the adversary’s power cannot be expressed simply in terms of number of nodes, because the network size is unknown. Instead, it is bounded by its commanding hashing power relatively to the total network hashing power. For instance, a \(30\%\)-bounded adversary (or simply \(30\%\) adversary) can solve PoW puzzles \(30\%\) of the time, while the remaining nodes together solve \(70\%\) of the time. Given this model, security is roughly understood as block immutability: if an honest node puts a block \(B\) on its blockchain, and \(B\) remains in the chain for some time, then all other honest nodes will do the same with high probability. This probability is typically quantified with confirmation length parameter \(k\), where \(1-e^{\Omega(k)}\) is considered reasonable security. \(k\) captures how long a block need to remain in the chain for it to be adopted by all honest nodes. In practice, the probability of tampering with a block grows exponentially smaller as honest nodes wait for more confirmation blocks.
| Notation | Definition |
|---|---|
| \(n\) | Number of nodes |
| \(\beta\) | Adversary bound |
| \(\alpha\) | Bound on honest nodes |
| \(\delta\) | Advantage of the honest node, \(\delta \geq \alpha/\beta\) |
| \(k\) | Confirmation length |
| \(f\) | Block interval: how fast a solution to PoW puzzle is found |
| \(\Delta\) | Propagation delay |
| \(\gamma\) | Rate at which honest node adopts blocks generated by the adversary |
| \(C^{\lceil k}\) | the chain obtained from cutting off the last \(k\) blocks of \(C\) |
The table above summarizes key notations for analysis. \(\beta\) is the number of Byzantine nodes in permissioned blockchains, and the relative hashing power in permissionless blockchain. It is easy to see why Bitcoin as well as other PoW blockchain cannot be secure when \(\beta > 50\%\). The specific attack here is that the adversary builds a private chain \(C_a\) which will be longer than the chain \(C_h\) the honest nodes are working on. At any time, the adversary can broadcast \(C_a\) and completely invalidates \(C_h\).
Security of traditional consensus protocols such as PBFT has been formally studied. Depending on network condition, classic BFT protocols require different bounds on the adversary. In fully asynchronous network, no consensus is possible (while also keeping liveness), due to the FLP result. The table below compares values of \(\beta\) necessary to achieve security. Recall that partiall synchronous means that there exists an unknown boundi \(\Delta\) on message delays; whereas synchronous means that that \(\Delta\) is known.
| BFT (synchronous) | BFT (partially synchronous) | PoW (synchronous & partially synchronous) | |
|---|---|---|---|
| \(\beta\) | \(\lfloor \frac{n}{2} \rfloor\) | \(\lfloor \frac{n}{3} \rfloor\) | \(50\%\) |
Effect of propagation time on Bitcoin security [1]
Decker et al. are the first to measure Bitcoin networks. Published in the P2P conference, just 5 years after the original Bitcoin paper, the paper contains a nice description of Bitcoin at the network level: how blocks and other messages are disseminated in the network.
-
Propagation time is defined as a time when a message is delivered to all nodes in the network. Without complete view of the network, the paper estimates it by connecting a number of clients to the real Bitcoin network. The client passively collects messages for a duration of \(10,000\) blocks. Using the message log, propagation time for a block can be estimated from the first time it was heard, until it was sent by all the client’s neighbors.
The measured propagation time is \(12.6s\) in average.
Using the same methodology, Gervais et al. [4] report a similar delay of \(\approx 9s\) (the difference is due to faster network in 2016 vs. 2013, and the use of Bitcoin relay network in the later study).
-
Probability of forks due to concurrency is modeled as
\[P_{fork} = 1 - (1 - f)^x\]where \(x\) represents the duration during which a node stayed uninformed of a new block. \(x\) is proportional, but not the same, as propagation delay, i.e. the higher the propagation delay, the higher is \(x\). Decker et al. estimated \(f \approx 1/633.68\) and \(x \approx 11.37\), making \(P_{fork} \approx 1.78\%\). Again, a similar result is confirmed later by Gervais et al.
-
An important interpretation of the fork model is that each time a block is found, an equivalent of \(x=11.37s\) mining is wasted. As a consequence, the effective total hash power is only \(1 - 11.37/633.8 = 98.2\). In other words,
The adversary bound decreases from \(50\%\) to \(49.1\%\).
We can devise a similar model for Ethereum where \(x\) is smaller (\(<1s\)) and \(f\) is higher (\(10-20s\)/block). Vitalk himself confirms the bound in Ethereum is only \(46\%\).
Selfish mining [2]
The study from Decker et al. basically refined the original security guarantees of Bitcoin; it is still a good approximation to say the adversary bound is \(50\%\). One year later, Eyal et al. presented the first important attacks on the system showing that \(\beta\) must be significantly lower. One implication of this paper is that a mining pool with \(25\%\) hash power is able to accumulate more share of the block rewards. But most importantly, it is able to lures honest miners to join the pool, thus snowballing the collective hash power beyond \(50\%\).
A mining pool consists of many miners, and is under control of one identity. It is easier to view a pool as a really powerful miner. The paper [2] is concerned with the scenario where mining pools go rogue. And the prognosis isn’t good.
Rational miners
When studying security of a distributed system, it is common to adopt the dichotomy of honest vs. malicious/Byzantine nodes, in which an honest node always follow the protocol correctly to the letter. When applied to cryptocurrencies setting, this model becomes too simplistic because miners are controlled by rational human agents who are out to maximize a certain objective function (a.k.a money). Eyal et al. therefore adopts a more realistic model that incorporate rational behavior. Although not cited in the paper, the model resembles the Byzantine Altruistic Rational (or BAR) model in classical consensus setting [7]. In particular, the network consists of three types of nodes:
-
Byzantine: the usual malicious node, whose only goal is to break things.
-
Altruistic: the usual honest node, who follows blindly.
-
Rational: the human-like node that adopt any strategy that maximizes its objective function.
The attack
The attacker is called a selfish miner, as its chief strategy involves withholding blocks instead of broadcast to the network.
Its ultimate goal is to increase the ratios of blocks in the blockchain that are generated by the adversary.
Given a blockchain \(C\), the number of blocks contributed by the adversary should be bound by its hashing power, i.e. \(\beta.len(C)\). Recall that \(\beta < \alpha\) (or else, we have simple \(>50\%\) adversary), a simplified version of the attack works as follows:
-
It mines on a private chain \(C'\) of block. The public chain on which honest miners are working is \(C\). Let \(L = len(C') - len(C)\) be the lead the adversary has over honest miners.
-
Selectively reveals the blocks in order to invalidate honest miners’ blocks:
2.1. When \(len(C) > len(C')\), it adopts \(C\) as the private chain. Thus, \(L>=0\).
2.2. With non-negligible probability, it finds a block \(B\) before honest miners, or \(L=1\). It keeps mining on \(C'\).
-
If honest miners find a block \(B'\), it immediately broadcasts its private block. This results in a probability of \(1-\gamma\) that \(B\) is adopted by the network.
-
If it again finds another block \(B''\), i.e. \(L = 2\), it continues mining on \(C'\).
2.3. With a lead of \(L>=2\) blocks, it broadcasts a private block for every block that the honest miners find. Because \(len(C') > len(C)\), at least \(L-1\) private blocks will be adopted by the network, wasting the honest miners’ effort in finding \(L-1\) blocks. \(L\) will be reduced to \(0\) eventually, since \(\beta < \alpha\), at which the adversary goes back to step 2.1.
-
Impact
The adversary’s relative block reward is directly proportional to the fraction blocks it can force to the blockchain. Eyal et al. devise a simple model for this relative reward, using just \(\beta\) and \(\gamma\). The result is shown in figure below.
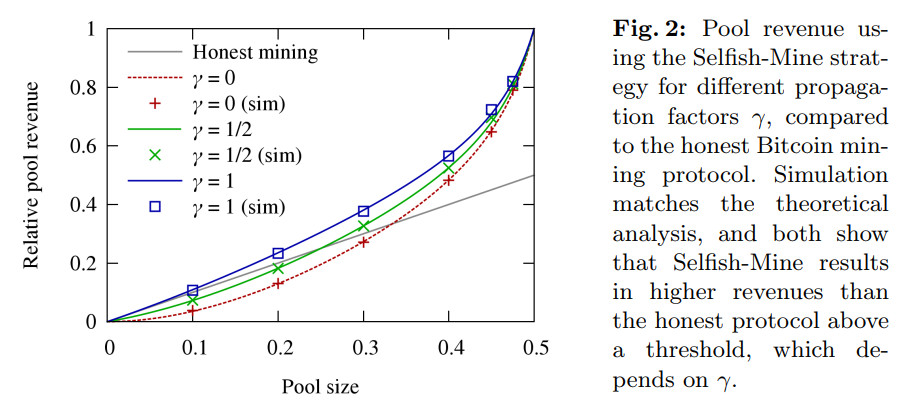
Two important take-aways are:
-
If the adversary can always convince another node of accepting its block in step 2.2.a, i.e. \(\gamma=0\), it relative reward is always better than honest mining. It means selfish mining is profitable.
-
If the adversary commands \(25\%\) of hashing power, and honest nodes adopts its block randomly with \(\gamma=0.5\), selfish mining is also profitable.
Take-away number 2 by itself doesn’t necessarily mean security is always compromised, because the adversary doesn’t have majority (\(\beta < 50\%\)).
However, under the BAR model it is almost the same as the adversary having majority of hashing power.
More specifically, selfish mining profitable means that honest mining is not rewarded fairly. In other words, the honest miners with a fraction of \(\alpha\) hashing power gets less than \(\alpha\) the block rewards. This motivates them to join the adversary in the latter mining pool, because it then get more reward than its fair share. At \(25\%\), the benefit of joining is already greater than \(0\). As the adversary pool gets bigger, the benefit grows faster than linearly (see the figure above), hence even more incentive to join. It’s only a matter of time before the adversary gets beyond the \(50\%\) threshold.
This work is clairvoyant
Written in 2014, many of the paper’s warnings did come true.
-
It warned that mining concentration is dangerous. New measurements of two biggest cryptocurrency network reveals that it is a real concern [6]. Although no mining pool has yet amassed \(25\%\), 6 largest Bitcoin pools now control \(90\%\) hashing power (11 pools in Ethereum respectively). A corollary is:
A Byzantine quorum system of 20 could achieve better decentralization than current PoW systems
-
Selfish mining did actually happen in a Japanese alt-coin. How is that for validation!
Security formalization [3]
Both [1] and [2] touched on the upper bound of the adversary power, beyond which is there no security. [1] says the bound is in fact strictly less than \(50\%\). [2] says \(\beta = 25\%\) is sufficient assuming the miners are rational. No work before [3] had formalized the relationship between \(\beta\) and security, or even defined exactly what security is. All 12 versions of the paper provides a formal model of the protocol which captures security with and without selfish mining. The newer versions also include partially synchronous communications. The model and proofs change quite a bit between versions; the following are based on the June 2017 version.
The model
The model follows a popular framework for analyzing security of multi-party computation. Fortunately I am not unfamiliar with this framework, thanks to months of pouring through pages and pages of Canetti’s universal composable (UC) security model — an incarnation of this framework — during the early years in my PhD. Granted, Garay et al.’s model is relatively more simple.
- A miner is an interactive Turing machine (ITM) with an input tape and output tape. It executes a protocol \(\Pi\), e.g. the Bitcoin backbone.
- A random oracle (RO) simulates PoW computation. A miner can query RO for a solution.
- Adversary control the communication channel and can tamper with the meta data the miners’ input tapes.
- All processing finishes within a round. In the synchronous setting, all messages are delivered in one round. In the partially synchronous setting, messages sent in round \(r\) is delivered before round \(r+\Delta\) (remember that \(\Delta\) is unknown to the miners).
An environment \(Z\) supplies input and issues queries to the miner. Its view \(V\), made up of the environment input and contents of the output tapes from the miners, is a random variable whose randomness comes from \(Z\)’s coins and the miners’. \(V\) represents the visible states of the entire network. Security of the protocol \(\Pi\) is specified as a predicate over \(V\). In particular, \(\Pi\) satisfies \(P\) if \(P(V)\) is false with negligible probability.
The protocol
The core of Bitcoin consists of three functions:
-
validate\((C)\): checks if content of the chain is valid. This involves checking validity of every block and the contained transactions, all the way back to the first block of \(C\). In practice, a miner would do this only incrementally by maintaining some indices. -
maxValid\((C_1,C_2,..)\): after receiving multiple chains from neighbors, selects one chain based on some pre-defined conditions. One condition is chain length, which captures the rule for resolving forks in Bitcoin. For example, if \(len(C_1) < len(C_2) ...\), it returns \(C_1\). -
pow(b,C): computes PoW solution for a new block content \(b\), using \(head(C)\) as the previous block. It sends up to \(q\) queries to RO per round, and gets a solution with probability \(f\).
The main loop at each miner is simplified as follows:
C = empty
round = 1
while True:
C' = maxvalid(C, any other chain C' found in input tape)
if found READ command:
write C' to output tape
b = new block found in input tape
C'' = pow(b, C')
if C'' != C:
C = C''
Diffuse(C)
else:
Diffuse(empty)
round++
It can hardly get any clearer than that.
Security property
So far we have to content with an informal description of security that is roughly equivalent to block immutability (see the earlier section). Now armed with the current model, security is defined as common prefix property. That is:
Common prefix (parameterized by \(k\)): for any two honest miners that output \(C_1\) and \(C_2\) at a round \(r\) in \(V\), it holds that \(C_1^{\lceil k} = C_2^{\lceil k}\)
where \(k\) essentially represents the confirmation length. This property says that the honest miners’ chains share a large prefix, which is non-empty when their chains are longer than \(k\) blocks. Let’s see how this implies block immutability: once an honest miner add a block \(B\) to its chain and \(B\) remains on the chain \(k\) blocks later, the common prefix property implies the (sub-)chain containing \(B\) is the common prefix shared by all honest miners.
Security property under selfish mining
Perhaps the greatest contribution [3] is that it captures selfish mining attacks via chain quality property. Recall the goal of selfish mining is to introduce as many blocks to the chain of honest miners as possible.
Chain quality (parameterized by \(l, \mu\)): for any honest miner that outputs \(C\) in \(V\), it holds that for any \(l\) consecutive blocks the ratio of adversarial blocks is at most \(\mu\).
\(l\) and \(\mu\) bound the impacts of selfish mining. For instance, if \(\mu > \beta\) selfish mining is profitable, hence honest miners are motivated to join the adversary. Note that this property says nothing about attack strategies. Therefore a bound on \(l, \mu\) will be the upper bound on selfish mining: the most clever attack can only claim up to \(l.\mu\) out of \(l\) blocks.
Proof highlights
The proofs for common prefix and chain quality are based on three random variables:
- A successful round \(X_i=1\) occurs when at least one honest miner finds a block in the round.
- A uniquely successfully round \(Y_i=1\) occurs when exactly one honest miner finds a block.
- An adversarial round \(Z_i=1\) occurs when the adversary finds a block.
Here is the high-level idea of the proof for common prefix. The first observation (see the paper for the exact lemma) is that the chain of a honest miner grows with \(X\). In particular, if at round \(r\) the chain length is \(l\), then at round \(r+s\) the chain grows to be at least \(l+\sum_{r}^sX_i\). Another observation is that if the \(k^{th}\) block of a chain \(C\) is generated by an uniquely successful round, then the \(k^{th}\) block of any chain \(C'\) will be either \(B\) or another block \(B'\) contributed by the adversary.
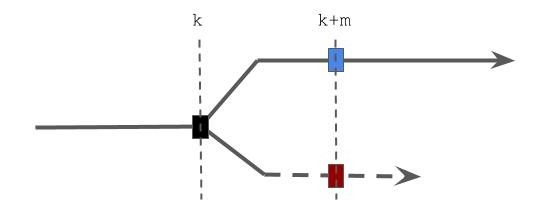
Let’s take a look at the figure above where the adversary tries to split the chain at block \(k\). The upper line represents the chain that honest miners work on, whereas the bottom is the adversary’s private chain. The first observation says that the upper chains will grow faster than the lower, because \(\sum_r^sX > \sum_r^sZ\) for round \(r < s\). Furthermore, if the block \(k+m\) in the private chain is generated in a uniquely private successful round, then in order to maintain the split the adversary is force to produce \(m\) different blocks from \(k\). Combined, the two observations suggest that to ensure common prefix, it is sufficient to set parameters such that the probability of the adversary being able to produce that many blocks to maintain the split is exponentially small. For example, if we can make the chain grow fast and there are many uniquely successful round, the adversary cannot catch up.
Main theorem (synchronous)
The following theorems provide sufficient conditions for achieving common prefix and chain quality. They are not necessary, in the sense that both properties can still be satisfied when those conditions are false.
Common prefix: if \(\frac{\beta}{\alpha} \leq (1-\delta)\) and \(\delta \geq 2f+\epsilon\) for some small \(\epsilon\), common prefix holds with \(k \geq 2 \eta\kappa f\)
and
Chain quality: if \(\frac{\beta}{\alpha} \leq (1-\delta)\) and \(\delta \geq 2f+\epsilon\) for some small \(\epsilon\), chain quality holds with \(\mu = (1+\delta/2).\frac{\beta}{\alpha}\) and \(l \geq 2\eta\kappa f\)
The sufficient condition \(\frac{\beta}{\alpha} \leq (1-\delta)\) and \(\delta \geq 2f+\epsilon\) can be interpreted as follows:
-
\(f \rightarrow 0\) corresponds to a setting in which it is hard to find a block in one round. In practice, it translates to a high ratio between block time and block propagation time. In this case, it is sufficient to set \(\beta\) close to \(\alpha\), i.e. \(\beta \approx 50\%\) in order to achieve common prefix. The ratio of adversarial block is close to \(\frac{\beta}{\alpha}\), which is strictly greater than \(\beta\). Hence, selfish mining is profitable. This bound is higher than what [2] observed. In particular, the specific attacks in [2] achieves a bound of \(<40\%\) when \(\beta = 33\%\). The result here suggests that it is possible to increase the adversarial block ratio up to \(50\%\). The paper in fact details an attack that achieves this bound.
-
\(f \rightarrow 0.5\) corresponds to a setting where it is very easy to find a block. In practice, it translates to a very small block interval. In this case, \(\delta \rightarrow 1\), meaning that \(\beta \rightarrow 0\). Therefore, the sufficient conditions for common prefix requires virtually all miners to be honest. Chain quality becomes quite high, but then it is expected because the adversary is almost non-existent.
Does it mean setting a small block interval, as Ethereum does, implies virtually no security? NO. The condition is only sufficient.
To the best of my knowledge, necessary conditions for security of PoW blockchains don’t yet exist. So if you’re out to design a new PoW blockchains, your best bet is to set your parameters such that the above sufficient conditions hold.
Main theorem (asynchronous)
Earlier versions of the paper used a rather unrealistic, fully synchronous model, in which all messages are delivered in the same round (and all processing done in the same round).
Let’s first extend it to a \(\Delta-\)synchronous model, where there is a known upper bound on message delay. Under this model, all miners simply wait \(\Delta\) rounds for all the messages. Traditional consensus protocols, e.g. BFT, treat this the same as fully synchronous. It’s the same as clocking down all the nodes such that they process messages \(\Delta\) times more slowly. No safety or liveness are affected. PoW consensus is different
In \(\Delta\)-synchronous model, the honest miner waits for \(\Delta\) round doing nothing, while the adversary can keep mining. Thus, \(\beta\) is increased by a factor of \(\Delta\).
As a consequence, for the sufficient conditions to hold, \(\beta\) mus be very small to start with. Or if \(\alpha, \beta\) were fixed at the beginning, and the network condition changes, both theorems above fail to hold (again, this doesn’t imply no security).
Now let’s move to the more realistic, partially synchronous model in which \(\Delta\) is unknown. Most practical, classic BFT consensus work in this model. The high-level ideas for proving common prefix and chain quality properties are similar as in the fully synchronous model. Here I’ll only summarize the results.
Common prefix: if \(\frac{\beta}{\alpha} \leq 1 - \delta\) and \(\delta \geq 3\Delta f + 5\epsilon + \frac{3\Delta}{\eta\kappa}\), then common prefix holds for \(k \geq 2f\eta\kappa + 2\Delta\)
Compared to the previous theorem, the lower bound on \(\delta\) is now increased by a factor of \(\Delta\). And the confirmation length is longer by \(O(\Delta)\) blocks. It means if for a given \(f\), in order for the sufficient conditions to hold, \(\frac{alpha}{\beta}\) must be \(\Delta\) time larger than before in the fully synchronous model. Another interpretation is that if \(\Delta\) becomes larger (corresponding to larger propagation delay in practice), \(\frac{\alpha}{\beta}\) must be \(\Delta\) times larger. For example, suppose \(f\) is small such that \(\beta \approx 50\%\), or \(\frac{\alpha}{\beta} \approx 1\) in the fully synchronous model. When \(\Delta=2\) the bound of the adversary reduces to \(\beta \approx 33\%\), and you’ll have to wait for \(4\) blocks longer.
Chain quality: if \(\frac{\beta}{\alpha} \leq 1 - \delta\) and \(\delta \geq 3\Delta f + 5\epsilon + \frac{3\Delta}{\eta\kappa}\), then chain quality holds with \(\mu = (1+\delta/2)\frac{\beta}{\alpha}\) and \(l \geq 2\eta\kappa f + \Delta\).
While common prefix deteriorates with higher \(\Delta\), chain quality looks better as the ratio of adversarial block, still bounded by \(\frac{\beta}{\alpha}\) is, lower than before. In practice this makes sense because with higher \(\Delta\), \(\beta\) is smaller, hence the adversary impact is also smaller.
Comparison to [8]
Pass et al. are first to analyse Bitcoin protocols in the partially synchronous model, which prompted Garay et al. to extend their early versions. I couldn’t follow the proof in [8] to the end, due to unfamiliarity with the formal model. But it appears that the results are similar, at least as far as interpretation and implication to real systems are concerned.
Quantitative security model [4]
Having stayed with me till this point, you may be wondering what are left to discuss, since security have been formalized and theorems proven (and I already said there’re not yet theorems about necessary conditions for security). Well, Gervais et al. set out to quantitatively study security properties in real systems, and quantify the trade-offs between security and transaction throughput. [4]’s high level contribution can be seen as validating the theorems and putting real numbers in the models.
Security = stale block rate
The wisdom in security is that you either have it or you don’t. In the real world, security must be measured and managed as risk. Garay et al. [3] define security as common prefix property, which is security in the traditional, binary sense. In contrast, Gervais et al. measures it in terms of stale block rate. This metric roughly approximates the risk of the common prefix property being violated. It is also a proxy for the risk of selfish mining, because the adversary introduce its blocks to the chain by means of stale blocks.
Real measurements
One very useful results of this work is the measurement of security-related parameters of real Bitcoin and Ethereum networks.
We can only control two parameters: block interval and block size.
I’m going to post the results in verbatim below.
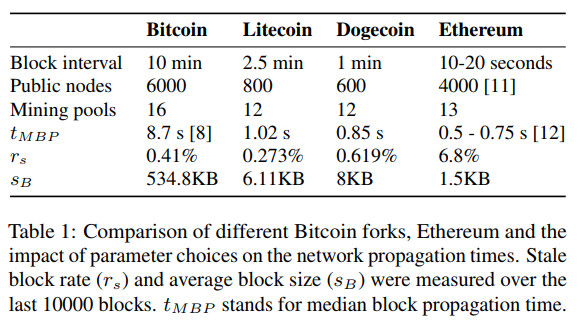
Note the similarity between the results an early work of Decker et al. [1].
Take-aways
I’ll not discuss the quantitative model (Markov Decision Process model) here, simply because I couldn’t understand it. But I’ll summary important take-aways from their simulation and how they are related to the theoretical results in [3].
-
The lower the block interval, the higher the stale block rate. This is as expected because higher \(f\) means there are more chance of concurrent blocks. In terms of security, when \(f\) is high the sufficient condition for common prefix to hold is that the adversary bound \(\beta\) becomes smaller. When \(\beta\) is smaller, there is less security in the sense that it is easy for the adversary to exceed this bound.
-
The larger the block size, the higher the stale block rate. This is the result of increased block propagation time as blocks get bigger, and the results in [3] imply that an increase in \(\Delta\) have the same effect as increase in \(f\). However, the interesting finding is
Block propagation time increases linearly up to 4MB, and exponentially after that.
which contrasts my initial impression that propagation time is linear to block size.
-
Efficient block propagation helps reduce stale block rate. This is consistent with [3], since lower \(\Delta\) means the adversary bound can be higher for the common prefix property to hold.
-
Throughput is a function of block size and block interval. But increasing one without lowering the other means lower security. The sweet spot for achieving the same security as current Bitcoin’s is \(f=60s\) and \(|B| = 1MB\), or \(\approx 67tps\).
Conclusion
The results above are guidelines for designing a secure blockchain system based on PoW consensus. They are not necessary conditions for security, but very useful nevertheless. Alternatives to PoW abound, and the models discussed so far could be easily generalized to them. In particular, the relative adversary power \(\beta\), block interval \(f\), propagation delay \(\Delta\), confirmation length, etc. are essential parameters in all of those PoW-like consensus.
References
[1] Decker et al. Information propagation in the Bitcoin network. P2P 2013
[2] Eyal et al. Majority is not enough: bitcoin mining is vulnerable. FC 2014
[3] Garay et al. The bitcoin backbone protocol: analysis and applications. Arxiv 2017
[4] Gervais et al. On the security and performance of proof of work blockchains. CCS 2016
[5] Dinh et al. Untangling blockchain: A data processing view of blockchain systems. TKDE 2018
[6] Gencer et al. Decentralization in Bitcoin and Ethereum network. FC 2018
[7] Aiyer et al. BAR fault tolerance for cooperative service. SOSP 2015
[8] Pass et al. Analysis of the Blockchain protocol in asynchronous networks. Arxiv 2016