Over the past 3 months I have finally came to face one of most important, yet most challenging (and feared) problems in distributed systems, namely distributed consensus. First raised in 1980s, the problem of getting a set of parties to agree on some value, remains an active area of research, with papers after papers appearing in top-tier systems conferences like SIGCOMM, NSDI, SOSP, OSDI. One may remark at the fact that researchers in the field have not reached a consensus on this decades-old consensus problem. Even without the human irrationality in the loop, the range of subtlety and unpredictability needed to be considered in solving consensus can perhaps be rivalled only by the human political systems. After all, there is no consensus on what is the best political system, and we as a race have worked on it since forever (and if this year is of any indication, we are failing specularly).

Like an enormous elephant in the room that one may try his best (but in vain) to ignore, the latest manifestation of distributed consensus is in the form of blockchain. At the heart of Bitcoin, Ethereum, Hyperledger, etc. is the protocol that ensures Byzantine fault tolerance: some participants are malicious and powerful, but the remaining honest participants (the majority) can still perform useful and correct work. As blockchain systems are gaining massive interest from the industry, this complex problem is again demanding attention.

As noted in another post I remember next to nothing of what was taught in the Distributed System course during my under graduate. But there are concepts that at the time I knew distinctively that I would forget. In fact, just recalling them by words bring up fields of darkness. Among them are leader election, Byzantine agreement, which I remember spending hours remembering the details of the long, inscrutable protocols without fully understand their relevant. To be fair, back then in 2005, these protocols were definitely reserved for the elite in the field. Raft [1], a popular consensus library which aims to bring the protocols to the mass, only appeared in 2014.

I will never be able to do justice to the complexity of distributed consensus and the vast design space it induces, and I do not plan to do so in this post. Instead, the following is merely a collection of notes I gathered from reading relevant papers.

Before moving on, let us get the definitions out of the way. Consensus protocol are characterized by two properties:

• Safety: all non-faulty nodes agree on the same value.
• Liveness: the system makes progress, i.e. it does not get stuck in any round of agreement.

They are so embedded into the design of existing large-scale systems that we may not see them being mentioned explicitly by names. Nevertheless, they are key to two major designs in distributed systems:

• Replication: data and application are replicated to increase availability and to tolerate failure. Replicas must agree on the same state for replication to be useful. The canonical example for this is replicated state machine.
• Partitioning: application states may be partitioned to increase load balancing and scalability. All the partitions must agree on the sequence of operations. The canonical example is a distributed, transactional database system.

FLP

There are inextricable links between consensus and fault tolerance. In fact, when there is no failure in the system, reaching consensus is rather straightforward. Most complexities arise from the requirement to tolerate failure. And whenever failure is possible, we are bound by the FLP impossibility result. That is, consensus (both safety and liveness) is not possible in asynchronous network. But of course this was not as negative as it sounded, since I am still here writing about this 30 years later.

Why then, despite FLP, are consensus possible in practice? The answer is two-fold:

1. Almost all consensus protocols choose safety over liveness, i.e. they are not live under network asynchrony. Some has claimed that liveness without safety is meaningless, but Bitcoin is an example of a live and probabilistically safe protocol, and Bitcoin is far from meaningless.

2. To achieve liveness, existing protocols assume the network is only partially asynchronous, i.e. a message sent repeatedly with a finite time-out will eventually be received.

So FLP still holds, but in practice assumptions can be made about the network to make consensus possible.

Two types of consensus

Consensus protocols differ widely in the types of failure they tolerate. One is non-Byzantine (or fail-stop, or crash) failure, in which faulty nodes simply stop responding (and later they will recover). Another is Byzantine, in which there are no restrictions to what faulty nodes can do. The former is popular in a distributed settings with a single owner (like a data center), whereas the later is similar to the open, decentralized settings like P2P networks. Almost all distributed databases adopt this fail-stop model. Byzantine failure models are often made in the context of security, particularly when nodes are compromised, or participants in the network are malicious.

Non-Byzantine

Paxos [4] and Viewstamped Replication (VR) [5] are the first two consensus protocols. They are essentially the same, with the latter being more easier to understand (and later implemented in Raft).

• The system progresses through a sequence of views, each view consists of a leader and a set of follower. The leader of view \(v\) is the one with ID \(v \ mod\ n\).
• In each view:
  • Client requests are sent to the leader.
  • Upon receiving a request, the leader broadcasts it to the followers.
  • The leader collects a majority of matching responses from the follower, replies to the client and commits to the request.
• View change is performed when either (1) leader fails, or (2) replicas time-out at processing requests.
  • View change protocol elects a new leader.
  • It is the most subtle part of the protocols, as commits from previous views must carry over to the new views.
• Checkpointing of the states are done periodically, to make state transferring and view change more efficient (as replicas must broadcast logs of previous operations).

This is similar to two-phase commit, but instead of waiting for responses from all replicas (hence not fault-tolerant), the leader only waits for a majority.

Why \((2f + 1)\) replicas (see notes at the end as well). To tolerate \(f\) crash failures, these protocols need \(2f+1\) replicas. This number is optimal, for the following reason. Because there can be \(f\) failures, there must be at least \(f+1\) in order for the request to be processed. If there is only 1 single agreement to be made, \(f+1\) is sufficient. However, we want the system to progress over multiple round, that is, whatever committed at round \(t\) is carried over to round \(t+1\). With this requirement, \(f+1\) replicas is not enough, since the non-faulty node at round \(t\) may be faulty at round \(t+1\), thus the operation processed at round \(t\) is lost. \(2f+1\) is the minimum number that offer quorum intersection, which guarantees that there is at least one node survive two consecutive rounds. In particular, the protocol requires responses from \(f+1\) replicas, say \((0,1,..,f)\), because then in the next round, even if \(f\) of them fail, there will be at least one replicas in \([0,f]\) present in majority quorum.

A more intuitive explanation is this: we want the operation committed at round \(t\) to survive into round \(t+1\), hence we need at least one node to survive the two rounds. To tolerate \(f\) failure, the quorum size must be at least \(f+1\) (since \(f\) of them may fail in the next round). The network size for which any two quorums of size \(f+1\) intersect at 1 node is precisely \(2f+1\) (set intersection property).

What happen to the remaining \(f\) replicas. The leader requires \(f+1\) replicas to response, because it assumes worst-case scenarios that the remaining \(f\) are faulty. After these faulty nodes recover, they can catch up with other via some kinds of synchronization.

Byzantine

The first major work considering non-crash failure models is Practical Byzantine Fault Tolerance (PBFT) [6] by Castro and Liskov in 1999 (a decade after Paxos). The paper is surprisingly easy to read in comparison to Lamport’s original Paxos paper, perhaps because it was presented as an extension to VR. In fact, the system also moves through a sequence of views, but there are a number of differences:

• Authenticated messages: unlike crash failure, nodes must be authenticated, to prevent malicious parties from creating or forging identities.
• In-view protocols: instead of 2 phases, there are now 3 phases of message exchange before replies can be sent to the client. Specifically:
  1. Client sends request to the leader.
  2. Leader broadcast PRE-PREPARE to followers.
  3. Each follower broadcasts PREPARE to other nodes, and waits for \(2f+1\) matching PREPARE messages (including its own).
  4. Each follower then broadcasts COMMIT to other nodes, and waits for \(2f+1\) matching COMMIT messages (including its own).
  5. Each follower executes the operation, then sends REPLY to the client. The client waits for \(f+1\) replies before returning.
• View changes: initiated by replicas when they detect/suspect leader failure, the new leader must prove that at least \(2f+1\) replicas (including itself) wanted a new view. Like in VR, view change is the most complex part of the protocol, and in this case it includes many large messages which carry signed proof and logs of previous operations.
• Checkpointing is carried out periodically, as in the non-Byzantine case.

Why \((3f + 1)\) replicas (see notes at the end as well). To tolerate \(f\) failures, at least \(3f+1\) replicas are needed. This number is optimal. Suppose we only have \(2f+1\) replicas and the protocol uses majority votes of \(f+1\). Suppose further that nodes \(0,1,..,f-1\) are faulty. In round \(t\), nodes \(f+1,..,2f\) do not receive messages (because of temporary network partition, may be caused by the Byzantine nodes), and the operation \(o_t\) is committed successfully in the quorum of nodes \(0,1,..f\). However, in round \(t+1\), node \(f\) is prevented from communicating with others, and the Byzantine nodes lie to non-faulty nodes that the last committed operation is \(o_{t'} \neq o_t\), which violates safety property. Thus, more replicas are needed to detect faulty nodes lying/equivocating. \(3f+1\) is the minimum size with the property that any quorum of \(2f+1\) replicas intersect at at least \(f+1\), hence at least 1 non-faulty node survive to the next round, even when the adversary can stop any arbitrary node from communicating

A more intuitive explanation for \(3f+1\) is the following. Unlike non-Byzantine protocols in which quorums need to intersect on 1 node, here the requirement is that the 1 node must be non-faulty. And because Byzantine node can lie arbitrarily, the only way to ensure that is to have the quorum intersection of size \(f+1\). Since \(f\) of them may fail in the next round, the minimum quorum size is \(2f+1\). And the network size for which any two quorums of size \(2f+1\) intersect at \(f+1\) nodes is precisely \(2(2f+1)-(f+1) = 3f+1\).

Recent works in non-Byzantine consensus

Following is a non-comprehensive list of recent, interesting works on non-Byzantine consensus.

• Fast Paxos: Lamport’s extension of Paxos that reduces the number of message delays/roundtrips from 4 to 3. Later works showed that it is actually not much faster than the original.
• Practical implementation: Raft [1] implements a version of the original VR protocol, optimizing for performance.
• Pushing down to the network: the networking communities are proposing to move some functionality (e.g. message ordering) of the protocols down to network layer, to exploit hardware performance and simplify the protocols themselves. This approach is made possible due to the availability of SDNs and programmable switches.
  • Paxos on switch: [7] implements Paxos protocols on P4, which could later be compiled and deployed directly on P4-compatible switches. Although no experimental results were presented, potential improvement in performance could only come from the direct use of different (faster?) hardware.
  • Speculative Paxos on Mostly-Ordered Multicast: [8]’s key design principle is to co-design network stack with the high-level applications (a recurring theme in this group from University of Washington). They first design a network primitive that guarantees ordered multicast messages with high probabilities (MOM). Albeit probabilistic, this MOM property allows for speculative execution of requests at the replica. The key insight here is that the major cost in Paxos (and in other consensus protocol) is in agreeing on the order of requests from the client, thus the protocol can be more efficient (and simple) if request ordering is taken care of by the network. Two direct benefits of this new protocol are: (1) shortening the number of message delays from 4 to 2 in normal case (no view change), (2) relieving the computation bottleneck at the leader. The trade-off here is that the client has to wait for a super-quorum (more than majority) before returning, and that the reconciliation protocols (including rolling back states) are expensive when replicas diverge due to message re-ordering.
    

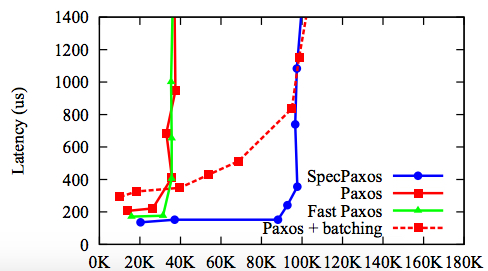
  Performance of Speculative Paxos (from [8]). Measured by increasing the number of closed-loop clients/threads (i.e. increasing the offered load). Flatter to the right is better

  • Consensus in a box: [9] implements atomic broadcast (ZAB), which is similar to Paxos, in FPGAs (commonly used to implement network middleboxes). Its key insight is that FPGAs can process messages at line-rate, plus application-specific network protocols (e.g. small-size messages, or point-to-point connections) can further boost the performance. The paper is filled with low-level implementation details, and the comparison against software implementation (Raft, Paxos) show expected gains.

  • NOPaxos: built by the same research group, [10] follows the same design principle of [8] by proposing a new network primitive that greatly benefits Paxos. The primitive is Ordered Unreliable Multicast (OUM), which guarantees ordered delivery or notification of message drop. It is realized via in-network serialization: instrumenting SDN to route messages to a centralized network processor which serializes requests and sends them to the group. The new Paxos protocol is more efficient than Speculative Paxos, because (1) client waits for smaller quorums of size \(f+1\), (2) guaranteed delivery means no reconciliation, no state roll-backs are needed. In case of unreliable delivery, i.e. message dropped cannot be recovered, the replicas revert to committing a no-op operations. The results show better throughput than Speculative Paxos, especially with message drop, and better latency (because of smaller quorums).

Recent works in Byzantine consensus

Following is a list of recent works in Byzantine fault-tolerant systems.

• Proof of work (or blockchain): Bitcoin [11], and recently Ethereum [12] usher in a wave of crypto-currency and blockchain systems. Targeting a decentralized, P2P system, a major contribution of these systems is their consensus protocols based on proof-of-works (PoW). The idea is incredibly simple: that the network select randomly at each round a node that proposes a value which the rest of the network adopts. Particularly, the probability of a node being selected is proportional to its ability to solve computation puzzles. The systems guarantees liveness, i.e. there will be solutions to the puzzles, but no safety. A value proposed by the selected node can only be agreed upon with a probability which can be made arbitrarily close to 1 after many rounds, unlike other BFT protocols which agreement (if reached) is absolute. PoW is computation bound (as opposed to other BFT protocols being communication bound), and its bottleneck is the overall hash power. Translating to energy cost, it’s been said that Bitcoin would consume as much electricity as the entire country of Denmark by 2020.

  Bitcoin’s and Ethereum’s popularity give strong evidence that fact that trading safety for liveness is acceptable in practice. In fact, in open, unauthenticated environments like the ones in which these system operate, PBFT and the related variants are not applicable. It is difficult to envision a completely safe protocol. Recent blockchain systems are moving towards a permissioned model with smaller numbers of authenticated nodes. And these private blockchains are turning to the literature for safe BFT protocols like PBFT (and the variants described below).

• Separating agreement from execution: [13] demonstrates two benefits of separating the origin PBFT into two sub-components: agreement and execution. One benefit is that it enables adding privacy firewall between the two to ensure execution confidentiality. But the main advantage I’ll discuss here is that it enhances modularity and helps reducing software errors that may lead to Byzantine failure. More importantly, it lowers quorum sizes for the servers that perform request execution. In particular, original PBFT protocol couples agreement and executing, thus requiring \(3f+1\) replicas. When separated into an agreement cluster and an execution cluster, the former first agrees on the order and then forwards it to the latter. The quorum sizes are as follows:

  • \(3f+1\) replicas in the agreement cluster to tolerate \(f\) failures.
  • \(2g+1\) replicas in the execution cluster to tolerate \(g\) failures. Why is it this small? Can Byzantine nodes lie about the next operation to be executed, like they can in the agreement cluster that necessitates \(3f+1\) replicas? No. In the agreement cluster, the leader may be faulty, and it can join the rest to lie about the next sequence number. But in the execution cluster, using the certified sequence number, a non-faulty node can know if there are gaps in the sequence of operations it has executed, and catch up or abort accordingly. Note here that faulty nodes cannot change the agreed sequence number, just we only need a majority quorum.

• Employing trusted hardware: the insight from [13], that ordering makes Byzantine consensus more efficient (smaller quorums), is extended further in [14, 15] with help of trusted hardware. Both systems employ hardware to prevent (detect) server equivocation, which is the root cause for needing \(3f+1\) in the agreement protocol. It can be seen that if a server cannot lie about sequence numbers it have proposed or executed, non-faulty nodes will always see and only agree on the latest sequence numbers. Enforcing unequivocation imposes serious handicap on Byzantine nodes, and like in [13], majority quorums out of \(2f+1\) are sufficient to tolerate \(f\) failures. Nevertheless, replicas incur extra overheads of detecting equivocation and of synchronous state-transferring during agreement.

  [15] implements the trusted components in FPGAs and demonstrates reasonable performance in normal cases. I wonder if new hardware like Intel SGX can offer any improvement.

• Speculative BFT: [16] proposes a variant of PBFT that speculatively execute the requests, even before replicas reach agreement. The system, named Zyzzyva, delivers very high performance in normal cases, by shortening the number of message delays. Specifically:
  • In the best case it uses 2 phases: leader broadcasts to the replicas, and the client collects \(3f+1\) matching response.
  • When the client receives \([2f+1, 3f+1)\) matching response, it broadcasts a commit request and waits for \(2f+1\) responses from the replica. This is similar to the COMMIT phase (step 4) in the original PBFT, which essentially makes sure that view change can make progress (or at least the honest node can detect others which are lying). Output of the COMMIT phase is that each replica has evidence that other \(2f\) are also committing to this operation. Without it, Byzantine nodes can lie.

  The view change protocol in Zyzzyva is rather involved, as it must compensate for the speculative execution (in the best case the replicas do not know that their executions are accepted by the clients). Compared to original PBFT, the client does more work.

• XFT: [17] makes clear distinction of node versus network failures, reasoning that there has not been powerful Byzantine adversaries that can cause network disruption in wide scale. Thus, the paper define anarchy as the system states where there are no correct ans synchronous majority of replicas, that is, the network is partitions and no partition contains the majority of non-faulty nodes. It then proposes XPaxos that works outside anarchy, i.e. there is a partition (within which the network is synchronous) containing at least \(f+1\) non-faulty nodes.

  Under this assumption, it appears quite straightforward that a variant of non-Byzantine protocol would work. In fact, XPaxos is very similar to Paxos, except that view change is carried out without a leader. This decentralized view change protocol ensures ordering across view (though I don’t fully understand why it cannot be done with a leader). The rather interesting part of how to select such synchronous partition for each view, however, is not described adequately (said in the paper that synchronous group is pre-defined, quite an unrealistic assumption). The protocol is then evaluated against Paxos and other BFT protocols including Zyzzyva. Compared to other BFT, it is clearly better, due the use of only \(2f+1\) replicas. It is worse than Paxos, due to the overhead from cryptographic operations, since in Paxos no authentication is needed.

  

  Performance of XPaxos (XFT) (from [17]). Measured by increasing the number of closed-loop clients/threads (i.e. increasing the offered load). Flatter to the right is better

---

Notes

Let \(N, Q, f\) be the number of replicas, quorum size and the maximum number of failures. While it is rather easy to derive \(Q\) when \(N = 2f+1\) (for non-Byzantine, or \(N = 3f+1\) for Byzantine failures), the following details more general property of \(Q\), especially with larger \(N\). It shows that going beyond the minimum \(N\) for tolerating \(f\) may be worse for performance.

Non-Byzantine quorum size

• To ensure liveness, one must be able to make progress (quorum to decide) without waiting for \(f\) failed nodes. That is, \(Q \leq N-f \leftrightarrow Q \geq \frac{N}{2} + 1\)

• To ensure safety, two quorums must intersect. That is, \(2Q > N\)

It follows that \(N < 2Q < 2(N-f)\). It means \(f < \frac{N}{2}\), or \(N> 2f\). It means the minimum size of \(N\) is \(2f+1\), and in this case \(Q > \frac{N}{2}\), or \(Q \geq f+1\).

Byzantine quorum size

• To ensure liveness, \(Q \leq N-f\)

• To ensure safety, two quorums must intersect at at least \(f+1\). That is \(2Q -f > N \leftrightarrow Q \geq \frac{N+f}{2} + 1\).

It follows that \(N < 2Q -f < 2(N-f)-f < 2N - 3f\). It means \(f < \frac{N}{3}\), or \(N \geq 3f+1\). At the minimum size of \(N\), i.e. \(N = 3f+1\), we have \(Q \geq 2f+1\).

References

[1] Raft: In search of an understandable consensus algorithm. https://raft.github.io/

[2] UoW notes: http://courses.cs.washington.edu/courses/csep552/16wi/

[3] MIT notes: http://people.csail.mit.edu/alinush/6.824-spring-2015/

[4] Paxos made simple.

[5] Viewstamped replication revisited.

[6] Practical Byzantine Fault Tolerance. OSDI 2009

[7] Paxos made switch-y. CCR 2016.

[8] Designing Distributed Systems Using Approximate Synchrony in Data Center networks. NSDI 2015.

[9] Consensus in a box: inexpensive coordination in hardware. NSDI 2016.

[10] Just say NO to Paxos Overhead: replacing consensus with networking ordering. OSDI 2016.

[11] Bitcoin: a peer-to-peer electronic cash system.

[12] Accelerating Bitcoin’s transaction processing: fast money grows on tree not on chain.

[13] Separating agreement form execution fo Byzantine Fault Tolerant Services. SOSP 2003

[14] Attested Append-Only memory: making adversaries stick to their words. SOSP 2007

[15] CheapBFT: resource efficient Byzantine fault tolerance. Eurosys 2012.

[16] Zyzzyva: speculative Byzantine fault tolerance. SOSP 2007

[17] XFT: pratical fault tolerance beyond crashes. OSDI 2016