History of the Impossibles - CAP and FLP
My undergraduate course in distributed systems was a disappointment. Starting the module (winter 2006) with anticipation of highly stimulating sessions, I was quickly let down by the materials. The textbooks were not the best, and the lecturers were clearly not passionate about the field. Over the next ten years, blind spots in my basic grasp of distributed systems kept revealing themselves. It was frustrating to encounter a (design) problem and have to work backward trying to reduce it to known principles. As much as the process helps remembering the principles better, I really wish the fundamentals were (better) taught in University.
This post is about my understanding of two principles in distributed systems underlying most of modern day designs. One is old and well formalized into theorems. The other is more recent but informal, crystallising wisdoms in building distributed systems.
Distributed System Models
Distributed systems are built over a network of nodes, so it is important to understand the network model, i.e. the assumptions of the network links.
-
Asynchronous model: the delay when sending a message from one node to another is finite but can be unbounded. In this model, a node cannot tell if its message is lost or being delayed. One consequence is that the node cannot use time-out/ping to detect failure. This model reflects worst-case communication, but it is simple and general.
-
Synchronous model: delay in sending a message is bounded, and finite by extension. It approximates more closely what we have today: the delay bound can be accurately estimated by sampling. This bound is used to determine whether the message is has been lost.
Network Partition - How the Network Fail
The difference between asynchronous and synchronous model can be better illustrated under network failure which is caused by link failure. Assume that the failure effectively partitions the network into two isolated sub-networks, such that messages exchanged between two nodes in different partitions are never delivered. Image there may be partition in the network, and the problem is to find out if partition really exists (and if yes, who are in the same partition).
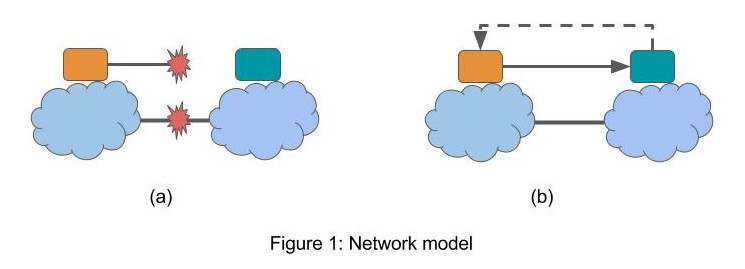
In Figure 1, the yellow node is trying to determines if there is partition, and whether the blue node is in the same partition with itself.
-
In the asynchronous model, delay can be unbounded therefore it is not possible to tell from a long delay whether it is caused by failure by the network being slow. In Figure 1, the yellow node cannot distinguish between (a) and (b) in finite time. It may set the timeout \(\delta\) to be very large, but it may happen that the message is delayed for \(\delta' > \delta\). Note subtly that even if the yellow node knows a priori that parition exists, i.e. it knows it’s in (a), it still cannot tell which nodes are in the same paritition.
-
In the synchronous, the timeout \(\delta\) is set to the network round trip time. When an acknowledgement is delivered within \(\delta\), the other node is indeed reachable and hence in the same partition. Otherwise, it can be safely assumed that the blue node is in another partition. In the figure above, (a) and (b) are distinct.
Thus, detecting network partition is straightforward in a synchronous network, but impossible in asynchronous network.
How Nodes Fail
A node can fail in one of two ways:
- Crash failure: it simply stops working, and never comes back on again.
- Byzantine failure: it does not stop working, but it behaves arbitrarily. This mode encompasses a wide range of misbehavior, either due to unintended bugs or malice.
Crash failure is much easier to deal with since the failed node can be in only one state — its behavior is predictable. Byzantine failure is notoriously difficult, since the failed node can be in any state. In some cases, Byzantine behavior adds noises to the overall executions. But in other cases it leads the executions to harmful states.
We are now ready to face the impossibles.
FLP - Agree to Disagree
In 1985, Michael J. Fisher, Nany A. Lynch and Michael S. Paterson published a seminal paper referred to as FLP. The paper concerned distributed consensus: the problem in which a number of nodes agree on a proposed value. A solution (or algorithm) to distributed consensus is characterized by 3 properties:
- Safety: the nodes agree on a valid value proposed by one of the node.
- Liveness: the nodes eventually reach agreement, i.e. the system must make progress.
- Fault-tolerance: the solution must work when there may be failure in the network.
The FLP roughly states that any solution to distributed consensus in asynchronous model can have at most 2 out of the 3 properties. In other words, no algorithms can be safe, live and fault-tolerant at the same time.
The surprise factor here is that it requires only one failure for the impossibility to take effect. Note that potential failure means there are cases when no failure is present (Figure 1b). But even in these cases the algorithm still cannot be safe and live at the same time. This may appear counter-intuitive at first: if there is no failure, then the algorithm does not have to be fault tolerance, hence the other two properties could be achieved, couldn’t it?
As a result, even when there is no failure, the algorithm still takes up the fault-tolerance property. If it can detect when failure is not presence, it can switch to another version that achieve both safety and liveness. But as we have already seen, it is not possible to detect failure in an asynchronous network, hence the algorithm must always be fault-tolerant.
CAP - Separation is Considered Harmful
In 2000 Eric Brewer, in an invited talk at PODC, proposed a principle later referred to as CAP theorem. Although in fact Brewer never called it a theorem, the unfortunate wording fueled subsequent confusions surrounding CAP. Initially presented as a conjecture, CAP concerns distributed, replicated storage systems which present illusions of single-copy data to large numbers of end users. I will discuss, in the following section, how such systems address a different problem to distributed consensus. CAP considers 3 properties in distributed, replicated storage.
- Consistency: specifies the semantics of read and write operations in distributed shared data systems. This is a concern when there exists multiple, concurrent writers and nodes may cache data. Many levels of consistency exist, but in CAP a strongest one — linearizability, that is read must see the latest value of write — is assumed.
- Availability: intuitively means the system should be able to serve requests. But it turns out to be the sources of most confusions about CAP, as Brewer was not explicit on his definition of availability. For now let us stick with the prevailing intuition.
- Partition-tolerance: similar to fault-tolerance in FLP, it means the system must handle network partitions (regardless of whether there actually is a partition or not).
The CAP conjecture states that distributed replicated storage systems can have at most 2 out of the 3
properties above. In other words, one cannot design a system which is consistent, available and fault-tolerant
at the same time. The conjecture captures what system designers had already known about designing distributed storage systems.
In fact, it is rather intuitive: when replicas cannot communicate, the system must either refuse requests
(non-available) or return stale (non-consistent) data. When replicas can communicate, it is possible to return
consistent data in finite time (for instance, a primary-backup design). Careful readers may notice a
discrepancy between the intuition and the original conjecture: “there is a partition” is not the same as “partition
tolerance”. The former is a property of the network, latter of the system itself.
FLP vs CAP - Chalk and Cheese
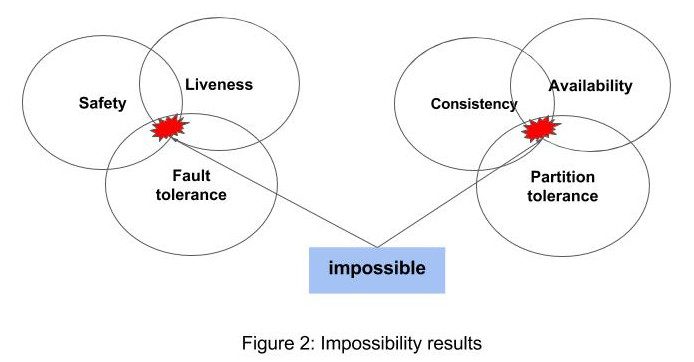 Figure 2 illustrates key take-aways from FLP and CAP. Both suggest that only 2 out of some 3 properties are possible.
They help filter out impossible designs at early stage, and their relation (or equivalence) is subject lengthy
discussions [1]. Here I would like to focus on a few notable distinctions.
Figure 2 illustrates key take-aways from FLP and CAP. Both suggest that only 2 out of some 3 properties are possible.
They help filter out impossible designs at early stage, and their relation (or equivalence) is subject lengthy
discussions [1]. Here I would like to focus on a few notable distinctions.
| Properties/Results | FLP | CAP |
|---|---|---|
| Problem scope | Distributed consensus | Replicated storage |
| Failure | Node crash fails | Network fails |
| Formalization | Rigorous | Gilbert & Lynch approximation |
| Solutions | Synchronous network model | No solutions exists |
Problem Scopes
Distributed consensus concerns the problem of having a number of nodes agree on a value. A common form of consensus is leader election, in which the nodes decide on the leader to coordinate the group. Another form is replicated state machine, in which the nodes agree on the sequence of events applied to a state machine. In databases, distributed commit is also a consensus problem: the nodes agree on whether to commit an operation.
Replicated storage is essentially a form of replicated state machine, in which states are memory locations and events are read and write operations. In this context, reaching agreement is important, but equally (if not sometimes more) important is concern of availability. For leader election and commitment, disagreement is not acceptable (all or nothing); but for replicated storage, refusing a read or write request can be worse than having diverge replicas.
One simple way to contrast these problems is that distributed consensus is often used when the task or data is partitioned/sharded over multiple nodes, whereas replicated storage is more suitable when the task or data is in multiple copies. Think 2PC in the first case, and primary-backup in the second.
Failure
FLP considers a node failing by crashing: it simply stops. CAP considers network failure causing partitions.
In the synchronous model, when a node failure is detected, it can be marked dead and removed from the system execution. However, when partition is detected, nodes in other partition cannot be marked as dead. Instead, both partitions must continue to work, but in isolation and while knowing that their states can diverge.
Formalization
FLP was formulated and shown rigorously in the I/O Automata framework, in which safety and liveness were defined formally. CAP, on the other hand, was initially presented as a conjecture and formalized only later on by Gilbert and Lynch (G&L) [2]. It is understandable, then, that there are gaps between what Brewer meant (or thought to have meant) and what were captured by G&L formal model. In fact, the main discrepancy lies in the definition of availability. Brewer’s conjecture implies an externally observed characteristic of the system, i.e. user-perceived uptime and delay. In G&L model, availability is a property of the algorithm, i.e. liveness. A G&L available system may take unbounded time to response, which is in counter to the pragmatics meaning of the word. I’ll come back to this later when discussing how CAP has evolved.
Impact
Both FLP and CAP help to rule out infeasible designs at early stage, to catch over-claims, and to identify system’s hidden flaws.
FLP identifies a fundamental problem with asynchronous network models: only one potential failure is necessary to eliminate consensus guarantees. As having consensus is at the heart of distributed systems, the result is a damaging one. Nevertheless, it has a flip side, that is it forces system designers to be explicit about the trade-offs: choosing either safety or liveness, and optimizing the other. More importantly, it raises the questions about asynchronous models. For example, FLP does not apply in synchronous models: it is possible to have all 3 properties at the same time. Thus, the natural question is: to which extent relaxing network asynchrony affects the trade-offs.
CAP was not entirely ground breaking at the time it came out, but it was quickly picked up by system designers. Although G&L’s proof put it in a formal ground, misunderstandings of the original conjecture and misinterpretations of the proof abounded. Brewer eventually wrote a paper to clarify his position [3], and there are paper as recent as December 2015 proposing extensions to CAP.
Unlike FLP which is solvable in synchronous networks, CAP is applicable regardless of the network models. In other words, even with bounded network delays, one still cannot have a consistent, available and partition-tolerance all at the same time (well, except for when there is no partition).
Living With FLP
Despite the negativity, FLP does not and have not stopped us building anything useful. First, FLP only shows that it is not possible to guarantee consensus under failure in asynchronous networks. It means that consensus can still be achieved some time. Particularly, a solution which trades safety for liveness or vice versa is far from being useless.
-
Safe but not live: 2-phase commit (2PC) trades liveness for safety, as it is important for databases/transactions to be in consistent states. Similarly, Paxos gives up liveness for safety: the algorithm may never terminate.
-
Live but not safe: 3-phase commit (3PC) trades safety for liveness: the algorithm always terminates, but there exists unsafe runs. More recently, Blockchain (exemplified by Bitcoin) implements a distributed consensus algorithm which always makes progress (new blocks are extended to the chain), but agreement is only probabilistic (the protocol waits for at least 6 extensions before a block is confirmed).
-
Safe and live: Technically one can modify 2PC by removing all fault-tolerance stuff (it never times out), thereby making it both safe and live. However, employing it in a real system is highly risky, since guaranteeing no failure is nearly impossible. If you chance reader happens to know of better examples please send me a note.
Overcoming FLP
FLP impossibility does not stop the community from creating robust consensus algorithms: both 2PC and Paxos are popular building blocks of today’s distributed systems. In fact, many view FLP with optimistic eyes: yes, it forbids a large portion of the design space, but the remaining space is vast and inviting.
- Failure detector: perhaps the most significant study after FLP is by Chandra and Toueg (CT), which explores how to
beat FLP by augmenting the asynchronous model. CT captured such augmentation in the form of a distributed failure
detector: each node can query its local failure detector to check whether another node has failed. This way, CT turned
consensus into an application which uses the failure detector. CT results, amid heavy formalization, are very neat:
- Consensus and atomic broadcast — the heart of Zab/Zookeeper — are equivalent.
- Consensus is possible in asynchronous settings if and only if it has access to a failure detector \(\Omega\). CT showed how to implement a form of consensus (leader election) using \(\Omega\).
- \(\Omega\) can be very weak: it may make infinite number of mistakes, but eventually it detects correctly at least one failure and does not mis-identify all non-failing node as failed.
Elegant as they are, failure detectors are purely a theoretical construct: it implies that solving consensus in asynchronous models is the same as building a weak failure detector \(\Omega\). CT emphasized many times in their paper that they are not concerned with implementation details of the detector. Of course \(\Omega\) cannot be built in asynchronous models, a direct consequence of FLP. Nevertheless, \(\Omega\) is possible to realize in other settings.
-
Synchronous models: one can build a perfect failure detector based on time-out. Take Paxos as an example, we can modify the algorithm to mark a node as fail when it fail to response within the time limit. The remaining nodes can then happily restart and proceed with the original algorithm.
-
Partially synchronous models : Dwork and Lynch explored the space in between wholly asynchronous and wholly synchronous models: the network is sometimes synchronous, sometimes asynchronous, but over time it stabilizes to synchronous [5]. They parameterized partial synchrony and identified cases in which it is possible to solve consensus. This study predated CT’s, and CT later demonstrated how to build \(\Omega\) in partially synchronous networks. Not only does the failure detector model agree with partial synchrony, it is more general, simple and intuitive.
Evolving CAP
The original CAP conjecture is intuitive for people who build distributed systems: when replicas are isolated by partitions, one must either return potentially inconsistent values or refuse requests. Since its first appearance, this version of CAP has undergone various refinements, clarifications and extensions to better capture subtle trade-offs embedded in the designs of existing systems.
CAP formalization
Gilbert and Lynch [2] spelt out important details omitted in Brewer’s presentation, namely the definition of network (a)synchrony, consistency, availability, partition tolerance. GL adopted as similar framework as in FLP, namely I/O Automata. They defined consistency as linearizability, available as liveness (response is generated eventually), partition tolerance as the ability to work when there may be network partition. Both asynchronous and synchronous models are considered.
Partition-tolerant algorithm (with P). Consider a partition-tolerant algorithm \(\cal A\): it must handle cases when there are network partitions.
-
In asynchronous models, it is not possible to have both A and C (Theorem 1). Less intuitive is that it is also impossible to have: (1) A in all executions and (2) C in executions without actual partition (Corollary 1.1.). I was struggling at first to understand this; because as far as my reasoning goes, if there is no partition, \(\cal A\) can just never time out thus eventually all updates will be delivered and the data can be both consistent and available (in the liveness sense). The flaw here is that this never-time-out algorithm is no longer fault-tolerant with A in all executions: it no longer has A in executions where there is partition.
- An example of AP algorithm is one that always returns a value from any replicas. Not very useful though.
- An example of CP algorithm is one that always forwards requests to a primary/master node. Not always available and scale poorly though.
-
In synchronous models, Theorem 1 still holds, as CAP is mainly influenced partition than by the presence of a failure detector (as with FLP). The same is not true for Corollary 1.1 no longer holds since it is now possible to design \(\cal A\) to have: (1) A in all executions and (2) C in executions without partition. Specifically, when detecting a partition (possible in synchronous networks), \(\cal A\) returns inconsistent values; otherwise it proceeds with normal consistency protocol (always terminates, i.e. available).
Non partition-tolerant algorithm (no P). Algorithms which ignore partitions are frown upon, for it is difficult to guarantee that the network never fails. In addition, such algorithms are rather trivial and therefore uninteresting. For example, the primary-backup algorithm without time-out is AC, because messages are never lost and the nodes simply wait. Though many would argue that data center networks can be assumed to have no partition, any design based on this strong assumption inevitably provokes doubts over its merits.
Many shades of CAP
GL made a great stride in dispelling most ambiguities surrounding Brewer’s conjecture. However, their formalization falls short of fully capturing the pragmatic understandings of the conjecture. Kleppmann in a recent paper [6] laid out several shortcomings of the formalization, focusing on the overly strict definitions of availability and consistency. Similar sentiments were voiced earlier by Brewer [3], in an attempt to thwart a seemingly prevailing misinterpretation of CAP. In the following, I only summarize Kleppmann’s ideas, more details are in [6].
Practically, availability is not the same as liveness. The former is an external property of an algorithm (measured in a continuous scale), the latter its internal (a binary property). Availability is usually stated in Service Level Agreements (SLAs): how much downtime, how long the service (response) latency is allowed. Liveness, on the other hand, requires only that the algorithm eventually generates responses. An algorithm with \(99.999\%\) uptime and sub-millisecond service time is definitely not live, because it fails to response to \(0.0001\%\) of the requests. Conversely, one which never refuses requests but takes hours/days/weeks to response is still considered live (though most would agree that it is not available). Although this mismatch by no means invalidates the GL proofs, it presents a sizable gap between Brewer’s definitions and what were captured in the formal model.
Like availability, consistency is not a binary property, but it comes in many different forms and definitions. In the context of replicated storage, there are at least 4 levels of consistency, listed in descending order from the strongest:
-
Linearizability: read must see the latest write, where latest is defined in relation to the global wall clock. This is a very strong property that even the CPU cache coherence protocol does not provide it.
-
Sequential consistency: the global order of read and write is consistent with the program order at each node.
-
Causal consistency: only causality (or partial order) among events is preserved.
-
Eventual consistency: if no writes occur in between, all reads eventually return the same value.
GL defined consistency as lineariability — an overly strong requirement in reality — and everything else as non-consistent. On the other hand, most large scale storage systems today, for instance Cassandra, are claiming some levels of consistency. Even the weakest, eventual consistency, is not the same as no consistency, as inconsistent values are later reconciled by upstream applications.
Given the non-binary nature of availability and consistency, the original trade-offs in CAP can be understood as not about choosing either C or A and completely sacrificing the other. As made clear in [3], it is about picking one and optimizing for the other under partition, and having all 3 when there is no partition (synchronous models are implicitly assumed here). Kleppmmann sums it up nicely:
Brewer’s informal interpretation of CAP is intuitively appealing, but it is not a theorem, since it is not expressed formally (and thus cannot be proved or disproved) – it is, at best, a rule of thumb. Gilbert and Lynch’s formalization can be proved correct, but it does not correspond to practitioners’ intuitions for real systems. This contradiction suggests that although the formal model may be true, it is not useful.
Latency-based CAP
Abadi [7] took the idea of having all C,A and P under no partitions (in synchronous settings) further and formulated it as PACELC. The principle is as follows: if there is Partition, choose one of Availability and Consistency, Else choose either Latency or Consistency. Abadi focused on the trade-offs between user-perceived latency and level of consistency, which arises when the algorithm has both A and C. PACELC is an extension of CAP, since one still cannot have A and C under partitions.
While CAP goes as far as saying that (binary) A and C are possible without partitions, PACELC says that even so, low latency and consistency are not possible at the same time. The A in PACELC seems to be the same as in GL’s proof. Latency therefore is an external manifestation of availability, a very long latency does not mean unavailable. Consistency here is still lineariablity. PACELC fits the intuition. When an algorithm wants low latency, it cannot afford consistency as the protocol is complex and involves exchanging messages. Conversely, when consistency is needed, latency must be long. PACELC captures in finer granularity the design space of many distributed storage systems. Cassandra and PNUTS, for instances, trade consistency for latency, as their read and write operations return quickly. VoltDB and other ACID databases, on the other hand, trade latency for consistency.
PACELC is intuitive, but it merely is an informal discussion. Kleppmann proposes to model availability in terms of latency — availability is the percentage of requests processed in a given period — thereby unifying the A and the L in PACELC. Furthermore, many consistency levels can be analyzed in terms of their asymptotic latency bounds. Thus, both AC and LC trade-offs can be expressed and studied via latency.
Concluding Notes
FLP is one of the most important results in computer science, whose impacts are keenly felt today at the heart of most distributed systems. Numerous follow-up works sprouted up after FLP, many of which are as important as FLP itself. In a way, CAP is a descendant of FLP, but it belongs to the more practical, engineering side of the family. CAP condenses wisdom in building systems which themselves are bound by FLP. Having experienced a rather bumpy development, it looks like CAP is coming to its end and being replaced by other conjectures.
[1] https://www.quora.com/Distributed-Systems-Are-the-FLP-impossibility-result-and-Brewers-CAP-theorem-basically-equivalent
[2] Gilbert and Lynch. Brewer’s conjecture and the feasibility of consistent, available, fault-tolerant web services.
[3] Brewer. CAP 12 years later: how the “rules” have changed.
[4] Chandra and Toueg. Unreliable failure detector for reliable distributed systems.
[5] Dwork and Lynch. Consensus in the presence of partial synchrony.
[6] Kelppmann. A critique of the CAP theorem.
[7] Abadi. Consistency trade-offs in modern distributed database systems.